RL basics
In a RL problem, we have an agent and an environment that the agent can interact with. At each time step, the agent is given a state of the environment \(s\), and the agent is supposed to take an action \(a\) to interact with the environment. Eventually, the agent will get a reward \(r\). The goal of the agent is to learn a policy \(\pi\), defined as \[ \pi(s, a) = \Pr[a~|~s]. \] which gives the probability of an action \(a\) being sampled at the given state \(s\).
Given a policy \(\pi\) and a starting state \(s\), we define the value of the state \(s\) to be the expected reward of starting from \(s\) with policy \(\pi\), hence the value function \(V^{\pi}(s)\) is defined as \[ V^{\pi}(s) := \mathbb{E}_{\pi}[\mathbf{R}_t ~|~ s_t=s] = \mathbb{E}_{\pi}\left[\sum_{k=0}^\infty\gamma^tr_{t+k+1} ~|~ s_t = s\right], \] where \(\gamma \in (0,1)\) is a reward decaying parameter and \(\mathbf{R}_t\) is defined to be the cumulative reward starting from time \(t\). Given a policy \(\pi\), a state \(s\) and an action \(a\), we can define the action-value function Q to be the expected reward of the state-action pair \((s, a)\), defined as \[ Q^\pi(s,a) := \mathbb{E}_\pi[\mathbf{R}_t~|~s_t=s,a_t=a]. \] Given the definitions, we have the following relation \[ V^\pi(s) = \sum_{a \in A}\pi(a~|~s)Q^{\pi}(s,a). \]
Markov Decision Process
If the environment state is a Markov process and there is a model describing the environment that for each triplet of a starting state \(s\), an action \(a\) taken and a ending state \(s'\), it gives the probability in the form of \[ \Pr(s', s, a) = \Pr[s_{k+1} = s'~|~ s_k = s, a_k= a]. \] then it is a Markov Decision Process, or MDP. It is a Model-based type RL problem.
Assume the reward is defined as \[ R(s', s,a) = \mathbb{E}[r_{k+1} ~|~ s_{k+1} = s', s_k = s, a_k= a]. \]
Bellman's Equations
For the value functions, we have \[ \begin{align*} V(s)=&~ \mathbb{E}_\pi \left[r_{t+1} + \sum_{k=1}^\infty\gamma^tr_{t+k+1} ~|~ s_{t} = s\right] \\ =&~ \mathbb{E}_\pi \left[r_{t+1} + \gamma V(s')~|~ s_{t} = s\right], \end{align*} \] where \(s'\) is a random state dominated by current state and action. Here we get a recursive expression named Bellman's Expectation Equation.
Again, our goal in RL is to find a policy, which maximizes the expected return from a starting state. Let's now define the partial order between the policies: if for all state \(s\), we have \(V^\pi(s) \ge V^{\pi'}(s)\), then we say \(\pi>\pi'\). In MDP with finite state set and action set, there exists at lease one policy \(\pi^*\) such that for any other policy \(\pi'\), it holds that \(\pi^*>\pi'\). We call it the optimal policy. With this, we can define the optimal value function \[ V^*(s) := \max_{\pi}V^{\pi}(s),~~\forall s \in \mathcal{S}. \] Also we can define the optimal Q function \[ Q^*(s,a) = \max_{\pi}Q^{\pi}(s,a),~~\forall s \in \mathcal{S}, a \in \mathcal{A}. \] To connect them, we have \[ \begin{align*} Q^*(s,a) =&~ r(s,a) + \gamma \sum_{s'\in\cal{S}}\Pr[s'~|~s,a]V^*(s') \\ V^*(s) =&~ \max_{a \in \cal{A}}Q^*(s,a). \end{align*} \] Hence we will have the following Bellman's Optimality Equation: \[ \begin{align*} V^*(s) =&~ \max_{a\in\cal{A}} \left\{r(s,a) + \gamma\sum_{s' \in \cal{S}}\Pr[s'~|~a,a]V^*(s')\right\} \\ Q^*(s,a)=&~ r(s,a) + \gamma\sum_{s'\in\cal{S}}\Pr[s'~|~s,a]\max_{a' \in \cal{A}}Q^*(s',s'). \end{align*} \]
Value Iteration
The goal of value iteration is to find the optimal value function \(V^*\). Starting from random (or all-zero) initialization, given Bellman's Optimality Equation, for every round, we update the value function by \[ \begin{align*} V^{k+1}(s) \gets &~ \max_{a}\sum_{s'}\Pr[s'~|~s, a]\left(r(s,a) + \gamma V^{k}(s')\right) \\ =&~\max_{a}Q^k(s,a) \end{align*} \] where \(\Pr(s', s, a)\) and \(r(s,a)\) are assumed known, and we use $ V^k$ and \(Q^k\) to represent the intermediate \(V\) and \(Q\) for approximating during the algorithm. We start by initiating \(\hat{V}\)'s for every \(s\) to be \(0\) or random. Then starting from a random state \(s_0\) and update the value by picking the action \(a\) that maximizes the value. Then we get to the next state. By iteratively doing this, we are able to finally construct good estimate to \(\hat{V}\)'s. When the values converges, we get the optimal policy \(\pi^*\) by \[ \begin{align*} \pi^*(s) =&~ {\arg\max}_{a}\sum_{s'}\Pr[s'~|~s, a]\left(r(s,a) + \gamma V^*(s')\right) \\ =&~{\arg\max}_{a}Q^*(s,a) \end{align*} \] It's a type of dynamic programming.
Policy Iteration
Here we start by locking the policy \(\pi\), and instead of updating optimal values by taking the best action like we did in value iteration, we update the value function with policy \(\pi\) by picking actions using \(\pi\). Like we did in the Bellman's Equation for optimal value functions \(V^*\)'s, we can get the same for \(V^\pi\): \[ \begin{align*} V^\pi(s)=&~ \mathbb{E}_\pi[R(s',s,\pi(s)) + \gamma V^\pi(s')] \\ =&~\sum_{s'}\Pr[s'~|~s, \pi(s)] \left(r(s,\pi(s)) + \gamma V^\pi(s')\right)\\ =&~ Q(s,\pi(s)) \end{align*} \] And we update policy by \[ \pi^{k+1}(s) = {\arg\max}_a \mathbb{E}[r(s,a) + \gamma V^{\pi_{k}}(s')] = {\arg\max}_aQ^{\pi_k}(s,a) \] Then we lock the policy and update the value functions. By iteratively doing this, we are able to get converged results.
Use of Q-function
By using Q function, the value iteration and the policy iteration can be summarized by simply \[ \begin{align*} V(s) =&~ \max_aQ(s,a) \\ \text{and}~~\pi(s) =&~ {\arg\max}_aQ(s,a). \end{align*} \] The good thing here is that Q function naturally encodes the information about the future so we can directly maintain its value instead of calculating value and pi each time.
Q-Learning
Q-learning is used when we don't have access of the model of the environment (model-free RL).
Monte Carlo Learning
We start from Monte Carlo Learning, which is the naive way (pure trial and error) of model-free RL. By the trials of the game, we have the cumulative reward over an episode \[ \mathbf{R}_t := \sum_{k = 0}^{n}\gamma^{k}r_{t+k+1}. \] Then update the value functions or Q functions by \[ \begin{align*} V^{\text{new}}(s_k) &~\gets V^{\text{old}}(s_k)+\frac{1}{n}\left(\mathbf{R}_k - V^{\text{old}}(s_k)\right)~~\forall k \in [n] \\ Q^{\text{new}}(s_k, a_k) &~\gets Q^{\text{old}}(s_k,a_k)+\frac{1}{n}\left(\mathbf{R}_k - Q^{\text{old}}(s_k,a_k)\right)~~\forall k \in [n] \end{align*} \] Mathematically this is not biased. So this in theory will finally converges. But it is relatively inefficient.
Temporal Difference Learning
TD learning integrates the information of time intervals, which can be connected with biological learning or some topics in neuroscience. We start with TD(0) learning. Recall the Bellman's Equation \[ V(s_k) = \mathbb{E}[r_k + \gamma V(s_{k+1})] \] Then in TD(0), we update the value function by \[ \begin{align*} V^{\text{new}}(s_k) &~\gets V^{\text{old}}(s_k)+\alpha\left(\overbrace{\underbrace{r_k + \gamma V^{\text{old}}(s_{k+1})}_{\text{TD target estimate }\mathbf{R_k}} - V^{\text{old}}(s_k)}^{\text{TD Error}}\right) ~~\forall k \in [n] \end{align*} \] For TD(N), we expand the value function as \[ \begin{align*} V(s_k) =&~ \mathbb{E}[r_k + \gamma V(s_{k+1})] \\ =&~ \mathbb{E} [r_k + \gamma r_{k+1} + \gamma^2V(s_{k+2})]\\ =&~ \mathbb{E} \left[\sum_{j=0}^N \gamma^j r_{k+j} + \gamma^{N+1}V(s_{k+N+1})\right] \end{align*} \] where we define \(\mathbf{R}^{(N)} := \sum_{j=0}^N \gamma^j r_{k+j} + \gamma^{N+1}V(s_{k+N+1})\). And hence the value function is updated by \[ \begin{align*} V^{\text{new}}(s_k) &~\gets V^{\text{old}}(s_k)+\alpha\left(\overbrace{\underbrace{\sum_{j=0}^N \gamma^j r_{k+j} + \gamma^{N+1}V^{\text{old}}(s_{k+N+1})}_{\text{TD target estimate }\mathbf{R_t}} - V^{\text{old}}(s_k)}^{\text{TD Error}}\right) ~~\forall k \in [n]. \end{align*} \] By letting \(N\) to the episode size or infinity, this converges to Monte Carlo learning.
There is another type of TD learning algorithms named TD-\(\lambda\), which calculates cumulative rewards from TD(0) to TD(N) and taking their weighted some in the following way \[ \mathbf{R}^{\lambda} := (1-\lambda)\sum_{n=1}^\infty \lambda^{n-1}\mathbf{R}^{(n)}. \]
Q-Learning
Q-Learning is temporal learning on Q functions, where in its TD(0) version, the Q functions are updated by \[ Q^{\text{new}}(s_k,a_k) \gets Q^{\text{old}}(s_k,a_k) + \alpha \left(r_k + \gamma\max_{a}Q^{\text{old}}(s_{k+1}, a)-Q^{\text{old}}(s_k,a_k) \right) \] Note that here we do not need necessarily to take the optimal action a to get to the next state, so this TD(0) Q-learning is off policy. In Q-learning, every time when the agent is about to take an action, a widely used way is by \(\epsilon\)-greedy policy, which means that it has a probability \(1-\epsilon\in(0,1)\) to take the best action, and \(\epsilon\) to take a random action from all the action space.
SARSA: State-Action-Reward-State-Action
SARSA is a variant of Q learning which is an on-policy algorithm, by updating Q functions in the following way \[ Q^{\text{new}}(s_k,a_k) \gets Q^{\text{old}}(s_k,a_k) + \alpha \left(r_k + \gamma {\color{red} Q^{\text{old}}(s_{k+1}, a_{k+1})}-Q^{\text{old}}(s_k,a_k) \right) \] SARSA also works with TD(N) for any \(N > 0\).
Deep RL
Deep Policy Network (Policy Gradient)
By introducing the neural network into the policy function, we use a network to approximate the policy, so a policy function parameterized by \(\theta\) can be written as \[ \pi_{\theta}(s,a). \] Then to update the policy \(\pi\), we update the parameters \(\theta\) by \[ \theta^{\text{new}} \gets \theta^{\text{old}} + \alpha \nabla_\theta \mathbf{R}_\theta \] We calculate the gradient here, first note that \(\nabla_{\theta}\mathbf{R}_\theta = \nabla_{\theta}V^{\pi_\theta}(s_0)\), where \(s\) is the starting state. By policy gradient theorem we have \[ \nabla_{\theta}V^{\pi_\theta}(s_0) \propto \sum_{s \in S}\nu^{\pi_{\theta}}(s)\sum_{a \in A} Q^{\pi_{\theta}}(s,a)\nabla_\theta \pi_{\theta}(a~|~s). \label{pg_thm1} \tag{1} \] The proof of policy gradient theorem can be found in this section. So we have \[ \begin{align*} \nabla_{\theta}V^{\pi_\theta}(s_0) \propto&~\sum_{s \in S}\nu^{\pi_{\theta}}(s)\sum_{a \in A} Q^{\pi_{\theta}}(s,a)\nabla_\theta \pi_{\theta}(a~|~s) \\ =&~ \sum_{x \in S}\nu^{\pi_{\theta}}(s)\sum_{a \in A} \pi_{\theta}(a~|~s)Q^{\pi_{\theta}}(s,a) \frac{\nabla_\theta\pi_{\theta}(a~|~s)}{\pi_{\theta}(a~|~s)} \\ =&~ \mathbb{E}_{\pi_\theta}[Q^{\pi_{\theta}}(s,a)\nabla_\theta\log \pi_\theta(a~|~s)] \end{align*} \] We can use it in the update of \(\theta\).
REINFORCE
In policy gradient, we need to know \(Q^{\pi_\theta}(s,a)\). There are multiple ways of estimating it. REINFORCE is a Monte Carlo variant of a policy gradient algorithm that estimates \(Q\) via sampling several steps. For example, in an environment with a finite steps (\(T\) steps), REINFORCE calculates the policy gradient by \[ \nabla_\theta V^{\pi_\theta} = \mathbb{E}_{\pi_\theta}\left[\sum_{t=0}^T\left(\sum_{t'=t}^T\gamma^{t'-t}r_{t'}\nabla_\theta\log\pi_{\theta}(a_t~|~s_t)\right)\right]. \] The algorithm runs in steps:
- Sample trajectory \(\{s_1,a_1,r_1,\dots,s_T,a_T,r_T\}\) using current \(\pi_\theta\);
- calculate return \(\hat{R}_t\gets\sum_{t'=t}^T\gamma^{t'-t}r_{t'}\) for every time step \(r\);
- update \(\theta\) by \(\theta_{\mathrm{new}}\gets \theta + \alpha\sum_{t=1}^T\hat{R}_t\nabla_\theta \log\pi(a_t~|~s_t)\).
Deep Q-Learning (DQN)
Just like Q-Learning, instead, model the Q function using neural network parameterized by \(\theta\), i.e., \[ Q(s,a) \approx Q_\theta(s,a) \] Recall that in Q-learning, we update Q value by \[ Q^{\text{new}}(s_k,a_k) \gets Q^{\text{old}}(s_k,a_k) + \alpha \left(r_k + \gamma\max_{a}Q^{\text{old}}(s_{k+1}, a)-Q^{\text{old}}(s_k,a_k) \right) \] So the loss here is defined as \[ L=\mathbb{E}\left[\left(r_k + \gamma\max_aQ_\theta(s_{k+1}, a) - Q_\theta(s_k,a_k)\right)^2\right] \] Here are some tricks of DQN.
experience replay:
In normal supervised learning, the data will be used to train the network for multiple times. However in DQN, each data is only used once. To avoid this, we maintain a buffer to store the 4-tuple of (state, action, reward, next state). When training, we pick batch of data from the buffer and use it to train the network.
target network:
The target of DQN is to approximate \(r + \gamma\max_aQ_\theta(s, a)\). Since the output of the network is included in the TD loss, it will be unstable during the training. To avoid this, we freeze the network by using a copy of it. Let's say original DQN to be \(Q_{\theta_1}(s,a)\) and a new network (target network) \(Q_{\theta_2}(s,a)\), the loss is then calculated as \[ L =\mathbb{E}\left[\left(r_k + \gamma\max_aQ_{\theta_1}(s_{k+1}, a) - Q_{\theta_2}(s_k,a_k)\right)^2\right]. \] The first network is updated using gradient descent, while the target network is only synced with the main network every \(C\) steps.
Another variant of Deep Q-Learning is Deep Dueling Q Network (DDQN), in which we split Q network into two parts, the value network \(V_{\theta_1}(s)\) and the advantage network \(A_{\theta_2}(s,a)\) such that \[ Q_\theta(s,a) = V_{\theta_1}(s)+A_{\theta_2}(s,a). \] By this, the value network learns the value function and the advantage network learns the advantage of an action could take to current state.
Actor-Critic Network
Recall that in Policy Gradient method, we calculated the gradient as following \[ \nabla_{\theta}J_\theta = \mathbb{E}_{\pi_\theta}[Q^{\pi_{\theta}}(s,a)\nabla_\theta\log \pi_\theta(a~|~s)]. \] Actually there is a generalized expression that \[ \nabla_{\theta}J_\theta= \mathbb{E}_{\pi_\theta}[\psi_t\cdot\nabla_\theta\log \pi_\theta(a~|~s)], \] where \(\psi_t\) can be one of
- \(\sum_{t'=0}^T\gamma^{t'}r_t'\): total return of the trajectory;
- \(\sum_{t'=t}^T\gamma^{t'-t}r_{t'}\): return after action \(a_t\);
- \(Q^{\pi_\theta}(s_r, a_t)\): Q function;
- \(A^{\pi_\theta}(s_t, a_t)\): advantage function;
- \(r_t+\gamma V^{\pi_\theta}(s_{t+1}) - V^{\pi_\theta}(s_t)\): temporal difference residual.
In Actor-Critic setting, we have two neural networks, one is policy network (actor) \(\pi_{\theta_1}(s,a)\) and the other is value network (critic) \(V_{\theta_2}(s)\). The loss of the value function is defined as \[ L(\theta_2) := (r+\gamma V_{\theta_2}(s_{t+1}) - V_{\theta_2}(s_t))^2. \] Like we did in the target network in DQN, the first part \(r+\gamma V_{\theta_2}(s_{t+1})\) is TD target and will not be calculated into gradient, we the gradient will be \[ \nabla_{\theta_2}L(\theta_2) = -2(r+\gamma V_{\theta_2}(s_{t+1}) - V_{\theta_2}(s_t))\nabla_{\theta_2}V_{\theta_2}(s_t). \] Hence the updated rule of the two networks are \[ \begin{align*} \theta_1 \gets&~ \theta_1 + \alpha_{\theta_1}\sum_{t}\delta_t\nabla_{\theta_1}\log\pi_{\theta_1}(a_t~|~s_t) \\ \theta_2 \gets&~ \theta_2 + \alpha_{\theta_2}\sum_{t}\delta_t\nabla_{\theta_2}V_{\theta_2}(s_t), \end{align*} \] where \(\delta_t := r_t +\gamma V_{\theta_2}(s_{t+1}) - V_{\theta_2}(s_t)\).
TRPO: Trust Region Policy Optimization [paper link]
All previous policy-based algorithms face a problem of instability during training. To avoid this, we consider a trust region when updating the parameters, with some security guarantee. Theoretically it can guarantee the monotonicity of performance during training.
Given current policy \(\pi_\theta\), we consider looking for a better parameter \(\theta'\) such that \(J(\theta') \ge J(\theta)\). Since the distribution of starting state \(s_0\) is independent of the policy. We can use expectation under new policy \(\pi_{\theta'}\) to describe current optimization target: \[ \begin{align*} J(\theta) =&~\mathbb{E}_{s_0}\left[V^{\pi_\theta}(s_0)\right] \\ =&~\mathbb{E}_{\pi_{\theta'}}\left[\sum_{t=0}^\infty\gamma^t V^{\pi_{\theta}}(s_t) - \sum_{t=1}^\infty\gamma^tV^{\pi_\theta}(s_t)\right] \\ =&~-\mathbb{E}_{\pi_{\theta'}}\left[\sum_{t=0}^\infty\gamma^t (\gamma V^{\pi_{\theta}}(s_{t+1}) - V^{\pi_\theta}(s_t))\right] \end{align*} \] Given this, we can calculate the difference between the two target functions as \[ \begin{align*} J(\theta') - J(\theta) =&~ \mathbb{E}_{s_0}\left[V^{\pi_{\theta'}}(s_0)\right] - \mathbb{E}_{s_0}\left[V^{\pi_\theta}(s_0)\right] \\ =&~ \mathbb{E}_{\pi_{\theta'}}\left[\sum_{t = 0}^\infty\gamma^t r(s_t,a_t)\right] + \mathbb{E}_{\pi_{\theta'}}\left[\sum_{t=0}^\infty\gamma^t (\gamma V^{\pi_{\theta}}(s_{t+1}) - V^{\pi_\theta}(s_t))\right] \\ =&~ \mathbb{E}_{\pi_{\theta'}}\left[\sum_{t=0}^\infty\gamma^t(r(s_t,a_t) + \gamma V^{\pi_{\theta}}(s_{t+1}) - V^{\pi_\theta}(s_t))\right] \end{align*} \] By defining temporal difference residual as the advantage \(A^{\pi_\theta}(s_t,a_t) := r(s_t,a_t) + \gamma V^{\pi_{\theta}}(s_{t+1}) - V^{\pi_\theta}(s_t)\), we have \[ \begin{align*} J(\theta') - J(\theta) =&~ \mathbb{E}_{\pi_{\theta'}}\left[\sum_{t=0}^\infty\gamma^tA^{\pi_\theta}(s_t,a_t)\right] \\ =&~ \sum_{t=1}^\infty \gamma^t\mathbb{E}_{s_t \sim P_t^{\pi_{\theta'}}, a_t\sim\pi_{\theta'}(\cdot~|~s_t)}[A^{\pi_\theta}(s_t,a_t)] \\ =&~\frac{1}{1-\gamma}\mathbb{E}_{s \sim \nu^{\pi_{\theta'}}, a\sim\pi_{\theta'}(\cdot~|~s)}[A^{\pi_\theta}(s,a)] \end{align*} \] where \(\nu^{\pi_\theta}(s)\) is the state visitation distribution, defined as \[ \nu^\pi (s):=(1-\gamma) \sum_{t=0}^\infty \gamma^tP_t^\pi(s), \] where \(P_t^\pi(s)\) is the probability that by policy \(\pi\), agent is at state \(s\) in time step \(t\). So we are now looking for a parameter \(\theta'\) with \(\mathbb{E}_{s \sim \nu^{\pi_{\theta'}}, a\sim\pi_{\theta'}(\cdot~|~s)}[A^{\pi_\theta}(s,a)] \ge 0\), then it will guarantee \(J(\theta') \ge J(\theta)\). But it is hard or impossible to solve this directly. So we ignore the difference between the state visitation distribution of the two policies and use the distribution of the old policy \(\pi_\theta\), hence we define the following optimization target \[ L_{\theta}(\theta') = J(\theta) + \frac{1}{1-\gamma}\mathbb{E}_{s \sim \nu^{\pi_{\theta}}, a\sim\pi_{\theta'}(\cdot~|~s)}[A^{\pi_\theta}(s,a)]. \] For the actions, we can use importance sampling and hence we get \[ L_{\theta}(\theta') = J(\theta) + \frac{1}{1-\gamma}\mathbb{E}_{s \sim \nu^{\pi_{\theta}}, a\sim\pi_{\theta}(\cdot~|~s)}\left[\frac{\pi_{\theta'}(a~|~s)}{\pi_{\theta}(a~|~s)}A^{\pi_\theta}(s,a)\right]. \] To make the policies are close enough, we use Kullback-Leibler Divergence constraint and hence we get the following optimization problem \[ \begin{align} \max_{\theta'}&~~L_\theta(\theta')\notag\\ \text{s.t.}&~~ \mathbb{E}_{s\sim\nu^{\pi_{\theta}}}[D_{KL}(\pi_{\theta}(\cdot~|~s), \pi_{\theta'}(\cdot~|~s))] \le \delta.\label{trpo}\tag{2} \end{align} \] The constraint here actually defines a KL ball in the policy space, called trust region.
PPO: Proximal Policy Optimization [paper link]
Consider the same optimization problem in TRPO \[ \begin{align*} \max_{\theta'}&~~\mathbb{E}_{s \sim \nu^{\pi_{\theta_k}}, a\sim\pi_{\theta_k}(\cdot~|~s)}\left[\frac{\pi_{\theta'}(a~|~s)}{\pi_{\theta}(a~|~s)}A^{\pi_{\theta_k}}(s,a)\right]\\ \text{s.t.}&~~ \mathbb{E}_{s\sim\nu^{\pi_{\theta_k}}}[D_{KL}(\pi_{\theta_k}(\cdot~|~s), \pi_{\theta'}(\cdot~|~s))] \le \delta. \end{align*} \] There are some methods to solve this optimization, including Taylor approximation, conjugate gradient method and linear search. But in general it is still hard to solve. So PPO was introduced. There are two types of PPO, PPO-Penalty and PPO-Clip.
PPO-Penalty
PPO-penalty use the method of Lagrange multipliers to put the constraint of KL divergence into the optimization function, hence we have the unconstrained optimization \[ \theta\gets {\arg\max}_{\theta'}\mathbb{E}_{s \sim \nu^{\pi_{\theta_k}}, a\sim\pi_{\theta_k}(\cdot~|~s)}\left[\frac{\pi_{\theta'}(a~|~s)}{\pi_{\theta_k}(a~|~s)}A^{\pi_{\theta_k}}(s,a) - \beta D_{KL}(\pi_{\theta_k}(\cdot~|~s), \pi_{\theta'}(\cdot~|~s))\right]. \] Let \(d_k = D_{KL}^{\nu^{\pi_{\theta_k}}}(\pi_{\theta_k}, \pi_{\theta'})\), the rule of updating \(\beta\) is
- If \(d_k < \delta/1.5\), let \(\beta_{k+1} = \beta_k/2\)
- If \(d_k >1.5 \cdot\delta\), let \(\beta_{k+1} = 2\beta_k\)
- else, let \(\beta_{k+1} = \beta_k\).
where \(\delta\) is a preset hyperparameter.
PPO-Clip
PPO-Clip is more straightforward, by restricting the difference of the policies directly in the optimization function using both, i.e., \[ \theta_{k+1}\gets {\arg\max}_{\theta'}\mathbb{E}_{s \sim \nu^{\pi_{\theta_k}}, a\sim\pi_{\theta_k}(\cdot~|~s)}\left[\min\left(\frac{\pi_{\theta'}(a~|~s)}{\pi_{\theta_k}(a~|~s)}A^{\pi_{\theta_k}}(s,a), \mathrm{clip}\left(\frac{\pi_{\theta'}(a~|~s)}{\pi_{\theta_k}(a~|~s)}, 1-\epsilon, 1+\epsilon\right)\cdot A^{\pi_{\theta_k}}(s,a)\right)\right]. \]
GAE: Generalized Advantage Estimation
In order to apply TRPO or PPO, we still need to know the values of advantage function \(A^{\pi_{\theta_k}}(s,a)\). One way we can approximate know the advantage is by GAE. Let \(\delta_t = r_t + \gamma V(s_t+1) - V_t\) be the temporal difference, where \(V\) is a learned value function. Hence we can define for different steps: \[ \begin{align*} A_t^{(1)} = &~\delta_t &= -V(s_t) + r_t + \gamma V(s_{t+1}) \\ A_t^{(2)} = &~ \delta_t + \gamma\delta_{t+1} &= -V(s_t) + r_t + \gamma r_{t+1}+\gamma^2 V(s_{t+2})\\ \vdots & &\vdots\\ A_t^{(k)} = &~\sum_{l=0}^{k-1}\gamma^l\delta_{t+1} &=-V(s_t) + r_t + \gamma r_{t+1}+\gamma^2+\dots+ \gamma^kV(s_{t+k}) \end{align*} \] And we calculate the weighted average over them to get: \[ \begin{align*} A_t^{\mathrm{GAE}} :=&~(1-\lambda)(A_t^{(1)}+ A_t^{(2)}+A_t^{(3)}+\dots) \\ =&~ (1-\lambda)(\delta_t + \lambda(\delta_t+\lambda\delta_{t+1})+\lambda^2(\delta_t+\lambda\delta_{t+1}+\lambda^2\delta_{t+2})+\dots) \\ =&~(1-\lambda)(\delta_t(1+\lambda+\lambda^2+\dots)+\gamma\delta_{t+1}(\lambda+\lambda^2+\lambda^3+\dots)+\dots)\\ =&~(1-\lambda)(\delta_t\frac{1}{1-\lambda}+\gamma\delta_{t+1}\frac{\lambda}{1-\lambda} + \gamma^2\delta_{t+2}\frac{\lambda^2}{1-\lambda} + \dots) \\ =&~\sum_{l=0}^\infty(\gamma\lambda)^l\delta_{t+l}, \end{align*} \] where \(\lambda \in [0,1]\) is a hyperparameter. For \(\lambda=0\), this becomes \(\delta_t\), and for \(\lambda=1\), this becomes average over \(A_t^{(k)}\)'s.
RL in Language Models
Some RL techniques are widely used in LLM alignment, though they are not intentionally designed for this.
RLHF: Reinforcement Learning with Human Feedback
It's hard to teach LLMs generating ``good'' text that aligns with human preference via regular Supervised Fine-Tuning (SFT). However, we can do that by RLHF. Typically, given a pretrained language model, there are several steps of RLHF:
- Gathering data by generating multiple responses from the LM, and use human annotation to rank the responses
- Train a reward model for predicting the human preference with future reward responses.
- Use RL methods to finetune the model to maximize the rewards, which will increase the probability of generating responses human like and decrease the probability of generating responses that human dislike.
Reward Modeling
Given a reward model \(R_{\theta}(q,a)\) parametrized by \(\theta\) and predict the rating of the question-answer pair \((q,a)\), following the Bradley-Terry model, which defines the probability that a rater prefers \(a_i\) over \(a_j\) as \[ \Pr[a_i \succ a_j] = \frac{\exp(R_\theta(q,a_i))}{\exp(R_\theta(q,a_i)) + \exp(R_\theta(q,a_j))}. \] Taking the negative log-likelihood of the probability, we get the training objective loss function for pairs \((q,a_i)\) and \((q,a_j)\) as \[ L(\theta) = -\log\sigma(R_\theta(q,a_i)) - \exp(R_\theta(q,a_j)). \]
PPO in RLHF
In this case, we typically train the critic model (used as value function) to be aligned with the output of the reward model. The objective can be written as \[ L(\theta_{c}) = \mathbb{E}_t[(V_{\theta_c}(s_t) - R_{\theta_r}(s_T))^2], \] where \(R_{\theta_r}\) is the pretrained reward model. And instead of using PPO-clip or penalty alone and optimize the objective function, we update the policy by calculating the loss of it to maximize the objective using both methods: \[ L_{\text{ppo}}(\theta) =\mathbb{E}_{s \sim \nu^{\pi_{\theta_k}}, a\sim\pi_{\theta_k}(\cdot~|~s)}\left[\min\left(\frac{\pi_{\theta'}(a~|~s)}{\pi_{\theta_k}(a~|~s)}A^{\pi_{\theta_k}}(s,a), \mathrm{clip}\left(\frac{\pi_{\theta'}(a~|~s)}{\pi_{\theta_k}(a~|~s)}, 1-\epsilon, 1+\epsilon\right)\cdot A^{\pi_{\theta_k}}(s,a)\right)\right] - \mathbb{E}_{s \sim \nu^{\pi_{\theta_k}}}\left[\beta D_{KL}(\pi_{\theta_k}(\cdot~|~s), \pi_{\theta'}(\cdot~|~s))\right] \] Adding them together, we get the loss function to optimize in RLHF using PPO: \[ L = L(\theta_r) + L_{\text{ppo}}(\theta). \]
GRPO: Group Relative Policy Optimization
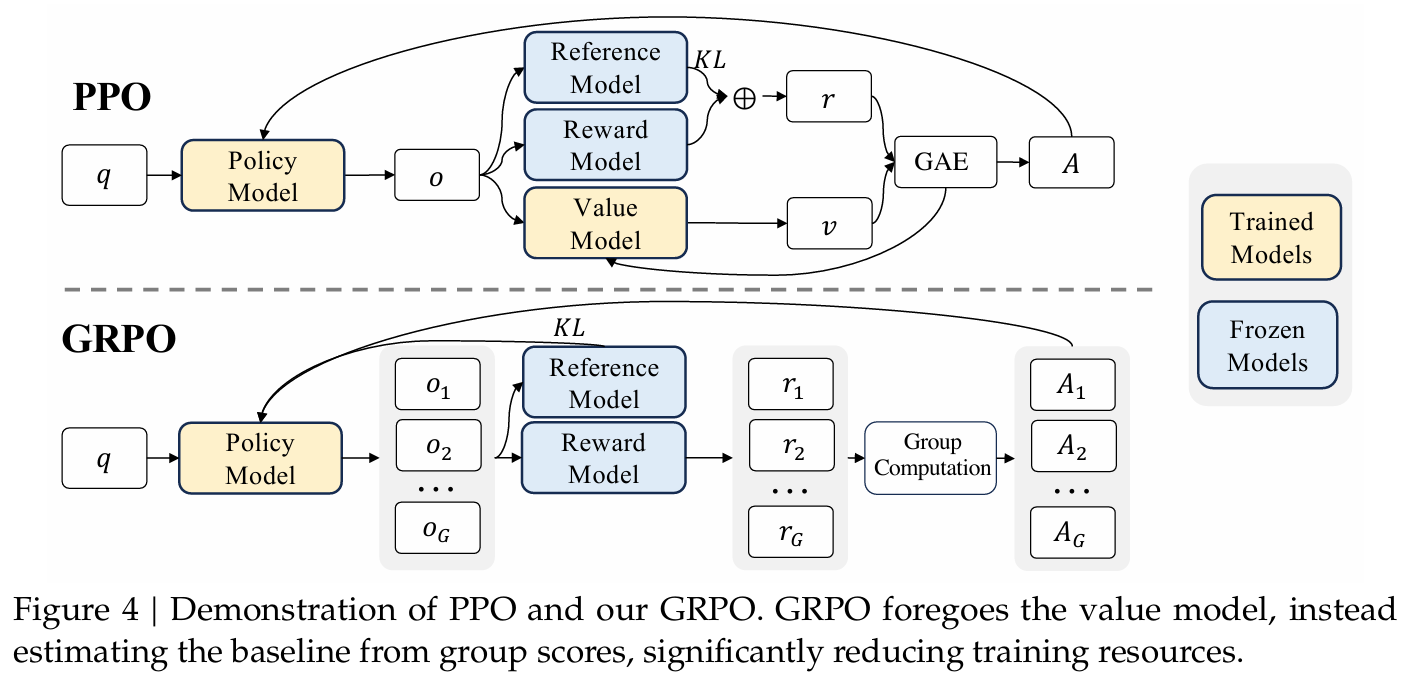
GRPO is proposed to avoid the use of the additional value function approximation. Specifically, for each question \(q\), GRPO samples a group of outputs \(\{o_1, o_2, \dots, o_G\}\) from current policy \(\pi_{\theta_k}\), then use them to optimize \[ \begin{align*} &L_{\text{GRPO}}(\theta) = \mathop{\mathbb{E}}\limits_{q\sim{\cal Q}, \{o_i\}_{i\in[G]}\sim\pi_{\theta_k}(\cdot~|~q)}\\ &\left[\frac{1}{G}\sum_{i=1}^G\frac{1}{|o_i|}\left\{\min\left\{\frac{\pi_{\theta}(o_{i,t}~|~q,o_{1,<t})}{\pi_{\theta_k}(o_{i,t}~|~q,o_{1,<t})}A^{\pi_{\theta_k}}_{i,t},\mathrm{clip}\left(\frac{\pi_{\theta}(o_{i,t}~|~q,o_{1,<t})}{\pi_{\theta_k}(o_{i,t}~|~q,o_{1,<t})}, 1-\epsilon, 1+\epsilon\right)A^{\pi_{\theta_k}}_{i,t}\right\}\right\}-\beta D_{KL}(\pi_\theta~|~\pi_{\theta_k})\right], \end{align*} \] where \(\epsilon\) and \(\beta\) are hyper parameters. The KL divergence here is estimated by unbiased estimator \[ D_{KL}=\frac{\pi_{\theta_k}(o_{i,t}~|~q,o_{1,<t})}{\pi_{\theta}(o_{i,t}~|~q,o_{1,<t})} - \log\frac{\pi_{\theta_k}(o_{i,t}~|~q,o_{1,<t})}{\pi_{\theta}(o_{i,t}~|~q,o_{1,<t})}. \] \(A^{\pi_{\theta_k}}_{i,t}\) is the advantage calculated based on relative rewards of the outputs inside each group only. For outcome based RL, i.e., the reward model outputs rewards based on the outcome for each of the outcomes \(\mathbf{r}:=\{r_1,r_2,\dots,r_G\}\), we assign the advantage of each internal token with the normalized reward, i.e., \[ \hat{A}_{i,t} \gets \frac{r_i-\mathrm{mean}(\mathbf{r})}{\mathrm{std}(\mathbf{r})}. \] For process based RL, i.e., the reward model outputs rewards based on every reasoning step of each outcomes \(\mathbf{R} :=\{\{r_1^{\mathrm{ind}(1)},\dots,r_1^{\mathrm{ind}(k_1)}\},\dots,\{r_G^{\mathrm{ind}(1)},\dots,r_G^{\mathrm{ind}(k_G)}\}\}\), where \(k_j\) is the \(\mathrm{ind}(j)\) is the ending token index of \(j\)-th step, and \(k_i\) is the total number of steps in the \(i\)-th output. We assign the advantage by \[ \begin{align*} \hat{r}_i^{\mathrm{ind}(j)} \gets&~ \frac{r_i^{\mathrm{ind}(j)}-\mathrm{mean}(\mathbf{R})}{\mathrm{std}(\mathbf{R})} \\ \hat{A}_{i,t} \gets&~ \sum_{\mathrm{ind}(j)\ge t}\hat{r}_i^{\mathrm{ind}(j)}. \end{align*} \]
Appendix
Proof of Policy Gradient Theorem
Here we give the proof for Eq.\(\eqref{pg_thm1}\).
We have \[ \begin{align*} \nabla_{\theta}V^{\pi_\theta}(s) =&~ \nabla_\theta\left(\sum_{a \in A}\pi_\theta(a~|~s) \cdot Q^{\pi_\theta}(s,a) \right) \\ =&~ \sum_{a \in A} \left(\nabla_\theta \pi_\theta(a~|~s)Q^{\pi_\theta}(s,a) + \pi_\theta(a~|~s)\nabla_\theta Q^{\pi_\theta}(s,a) \right)\\ =&~ \sum_{a \in A} \left(\nabla_\theta \pi_\theta(a~|~s)Q^{\pi_\theta}(s,a) + \pi_\theta(a~|~s)\nabla_\theta \sum_{s',r}\Pr[s',r~|~s,a](r+\gamma V^{\pi_\theta}(s')) \right)\\ =&~ \sum_{a \in A} \left(\nabla_\theta \pi_\theta(a~|~s)Q^{\pi_\theta}(s,a) + \gamma \pi_\theta(a~|~s)\sum_{s',r}\Pr[s',r~|~s,a]\gamma \nabla_\theta V^{\pi_\theta}(s') \right)\\ =&~ \sum_{a \in A} \left(\nabla_\theta \pi_\theta(a~|~s)Q^{\pi_\theta}(s,a) + \gamma \pi_\theta(a~|~s)\sum_{s'}\Pr[s'~|~s,a]\gamma \nabla_\theta V^{\pi_\theta}(s') \right)\\ \end{align*} \] Define \(\phi(s) := \sum_{a \in A}\nabla_\theta\pi_\theta(a~|~s)Q^{\pi_\theta}(s,a)\). Define \(p^{\pi_\theta}(s \rightarrow x, k)\) to be the the probability of policy \(\pi\) starting from state \(s\) to arrive at state \(x\) after \(k\) steps. Hence we have \[ \begin{align*} \nabla_{\theta}V^{\pi_\theta}(s) =&~ \phi(s)+\gamma\sum_{a\in A}\pi_\theta(a~|~s)\sum_{s'}\Pr[s'~|~s,a]\gamma \nabla_\theta V^{\pi_\theta}(s') \\ =&~ \phi(s) + \gamma \sum_{a \in A}\sum_{s'} \pi_\theta(a~|~s)\Pr[s'|s,a]\nabla_\theta V^{\pi_\theta}(s') \\ =&~ \phi(s) + \gamma \sum_{s'}p^{\pi_\theta}(s \rightarrow s', 1)\nabla_\theta V^{\pi_\theta}(s') \\ =&~ \phi(s) + \gamma \sum_{s'}p^{\pi_\theta}(s \rightarrow s', 1)\left(\phi(s') + \gamma\sum_{s''}p^{\pi_\theta}(s \rightarrow s'', 2)\nabla_\theta V^{\pi_\theta}(s'')\right) \\ =&~ \phi(s) + \gamma \sum_{s'}p^{\pi_\theta}(s \rightarrow s', 1)\phi(s') + \gamma^2 \sum_{s''}p^{\pi_\theta}(s \rightarrow s'', 2)\nabla_\theta V^{\pi_\theta}(s'') \\ =&~ \cdots \\ =&~ \sum_{x \in S}\sum_{k=0}^\infty \gamma^k p^{\pi_\theta}(s \rightarrow x, k)\phi(x). \end{align*} \] Define \(\eta(s) = \sum_{k=0}^\infty \gamma^k p^{\pi_\theta}(s \rightarrow x, k)\). We get \[ \begin{align*} \nabla_\theta V^{\pi_\theta}(s) =&~ \sum_{x \in S}\eta(x)\phi(x) \\ =&~ \underbrace{\sum_{x \in S}\eta(x)}_{\text{Constant}} \cdot \sum_{x \in S}\frac{\eta(x)}{\sum_{x \in S}\eta(x)}\phi(x) \\ \propto&~ \sum_{x \in S}\frac{\eta(x)}{\sum_{x \in S}\eta(x)}\phi(x) \\ =&~ \sum_{x \in S} \nu^{\pi_\theta}(s) \sum_{a \in A}Q^{\pi_\theta}(s,a)\nabla_\theta\pi_\theta(a~|~s), \end{align*} \] where \(\nu^{\pi_\theta}(s)\) is the state visitation distribution, defined as \[ \nu^\pi (s):=(1-\gamma) \sum_{t=0}^\infty \gamma^tP_t^\pi(s), \] where \(P_t^\pi(s)\) is the probability that by policy \(\pi\), agent is at state \(s\) in time step \(t\).